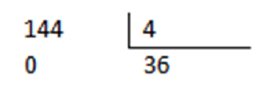CRITERIO DE DIVISIBILIDAD POR 4
Para construir el criterio de divisibilidad por 4, necesitamos observar cómo se comportan los múltiplos de 4, observaremos los primeros 90 múltiplos:
Sabemos que todos los múltiplos de un número son divisibles por ese mismo número. Por ejemplo 144 es múltiplo de 4 (4x36 = 144) por lo tanto 4 divide exactamente a 144:
* Ahora observemos en la tabla de los múltiplos de 4 presentada anteriormente, la cifra que ocupa la posición de las unidades en cada uno de los múltiplos.
¿Qué tienen en común las cifras de las unidades de todos los múltiplos de 4?
SON NÚMEROS PARES
* Seguiremos observando en los múltiplos de 4, esta vez el número que ocupa la cifra de las decenas:
¿Podemos clasificar como pares o impares los números que ocupan la cifra de las decenas de todos los múltiplos de 4? NO, PUES HAY TANTO PARES COMO IMPARES.
* Vamos a observar la cifra de las decenas de todos múltiplos de 4, que terminen en 0:
¿Qué tienen en común las cifras de las decenas de todos los múltiplos de 4 que terminan en 0?
SON NÚMEROS PARES
* Ahora observaremos la cifra de las decenas de todos los múltiplos de 4 que terminan en 4:
¿Qué tienen en común las cifras de las decenas de todos los múltiplos de 4 que terminan en 4?
SON NÚMEROS PARES
* Ahora observaremos la cifra de las decenas de todos los múltiplos de 4 que terminan en 2,6 y 8:
¿Qué tienen en común las cifras de las decenas de todos los múltiplos de 4 que terminan en 2?
SON NÚMEROS IMPARES
¿Qué tienen en común las cifras de las decenas de todos los múltiplos de 4 que terminan en 6?
SON NÚMEROS IMPARES
¿Qué tienen en común las cifras de las decenas de todos los múltiplos de 4 que terminan en 8?
SON NÚMEROS PARES
* De acuerdo a las características observadas formaremos el criterio de divisibilidad por 4:
CRITERIO DE DIVISIBILIDAD POR 8
Para construir el criterio de divisibilidad por 8, necesitamos observar cómo se comportan los múltiplos de 8, observaremos los primeros 90 múltiplos:
Para saber si un número de dos cifras es divisible por 8 es necesario saber la tabla del 8 hasta el 12, pues la regla de divisibilidad por 8 que construiremos aplica con números de tres cifras en adelante.
* Observemos en orden de fila las últimas dos cifras de los múltiplos de 8:
¿Qué descubrimos con respecto a las dos últimas cifras de los múltiplos de 8? R/ Las dos últimas cifras de los múltiplos de 8 forman un número divisible por 4.
* Haremos una comparación entre los múltiplos de 4 hasta 96 y los múltiplos de 8 hasta 96:
De la comparación que se hizo ¿Qué podemos asegurar? R/ Que hay múltiplos de 4 que también son múltiplos de 8.
* Con esta característica bien clara, realizaremos una observación similar a la que hicimos en el criterio de divisibilidad por 4, pero esta vez observaremos el número que antecede a las dos últimas cifras (cifra de las centenas) según sea que sus dos últimas cifras formen un número que aparezca en la tabla del 4 y del 8, o bien sólo en la del 4; además un caso especial cuando el múltiplo de 8 termina en doble cero:
¿Qué tienen en común los múltiplos de 8, que terminan en número de dos cifras que aparece en la tabla del 4 y del 8, con respecto a la cifra que ocupa la posición de las centenas? R/ El número que ocupa la posición de las centenas para estos múltiplos de 8 ES UN NÚMERO PAR.
¿Qué tienen en común los múltiplos de 8, que terminan en número de dos cifras que aparece en la tabla del 4 y no en la del 8, con respecto a la cifra que ocupa la posición de las centenas? R/ El número que ocupa la posición de las centenas para estos múltiplos de 8 ES UN NÚMERO IMPAR.
¿Qué tienen en común los múltiplos de 8, terminados en doble cero, con respecto a la cifra que ocupa la posición de las centenas? R/ El número que ocupa la posición de las centenas para estos múltiplos de 8 ES UN NÚMERO PAR.
* De acuerdo a las características observadas formaremos el criterio de divisibilidad por 4: